分光器の光学設計2 補足トピック - 光学設計とその周辺、そしてたまに全く関係ないやつ

前回の記事ではチェルニタナー光学系の設計方法について扱いました.

eikonal.hatenablog.jp

今回は他の細かいトピックを扱ってみます.

スループット

前回の記事では触れませんでした, 光学系がもつスループット(集光効率), どれだけ分光器光学系が光を集光できるかを考えます.

いつかの記事でも扱いましたが輝度 $L$ , 微小面積 $\Delta S$ ,立体角 $\Delta \omega$ における光量 $\Phi$ は以下の式で表せます. nは媒質中の屈折率を表しますが基本的にはn=1として進めます.

$\displaystyle \Phi=L n^2 \Delta \omega \Delta S \tag{1-1} \label{1-1}$

これを使って入射スリットに輝度Lの光が入射したときにセンサー位置の光量を求めていきます.

まず $\Delta \omega$ ですが焦点距離fのコリメーターミラーが光束を回折格子上に半径hの円で照射するような場合, 近軸の範囲で以下の通り表されます.

$\displaystyle \Delta \omega=2\pi(1-\cos{\theta})\approx \pi \theta^2 = \pi (h^2/f^2) \cos{\alpha} \tag{1-2} \label{1-2}$

一方, $\Delta S$ については入射スリットの幅そのものにもちろんなりますが, 前回の記事の式(6)より,半値幅の仕様 $\Delta \lambda$ から相当するスリット幅wが求められます.

以上をまとめると,スリット長さをHとすると,光量 $\Phi$ は以下の通りになります.

$\displaystyle \Phi=L \Delta \omega \Delta S =L \pi (h^2/f^2) \cos{\alpha} \frac{Gf_C}{\cos{\alpha}} \Delta \lambda H=L \frac{\Delta \lambda}{\lambda} \frac{\pi h^2}{f^2} (f_C H) (\sin{\alpha}+\sin{\beta}) \tag{1-3} \label{1-3}$

最後の項については回折格子の式から変換しました. この式から分光器のスループットを高める方法を考えます. $\Delta \lambda/\lambda$ は半値幅に関する項ですので, 仕様から自動的に決まります. $h^2/f^2$ はF値に関する項ですので大きくしようにもある程度の限界はあります. $f H$ の項はいわば光学系のサイズに関する項ですがfは要求されるサイズからある程度制約のある値ですしHももちろん大きくすることはできますがポリクロメーターの場合は現実的にはディテクターのラインナップに制限されます. 一方最後の項は多少は利用できる余地はあるかもしれません. 角度の大きさはm=1次式を使う場合, 通常は $| \alpha | > | \beta |$ ですので, $\sin{\beta}$ を思い切って無視すれば, 要は回折格子への入射角を大きくすると光量が得られるということになります. ただもちろん回折効率の入射角特性など他にも諸々考慮しないといけません.

偏心時の焦点距離

焦点距離は通常軸上で定義される値ですが, 偏心すると非点収差の影響で焦点距離に相当するものが画角により変わります. 以下の図で曲率半径rをもつミラーに光軸から $\theta$ で入射し, $\theta'$ で出射する点の結像を考えた際, 以下の式が成り立ちます. Oが無限遠にある場合はa->0とすればbが求まります.

メリジオナル面

$\displaystyle \frac{\cos^2{\theta}}{a}-\frac{\cos^2{\theta'}}{b} =\frac{-\cos{\theta'}-\cos{\theta}}{r} \tag{2-1} \label{2-1}$

サジタル面

$\displaystyle \frac{1}{a}-\frac{1}{b} =\frac{-\cos{\theta'}-\cos{\theta}}{r} \tag{2-2} \label{2-2}$

特に偏心した分光器光学系の特徴ですが, 像面では偏心のある方向(波長が分散される画素が並ぶ方向)については点像広がりがそのまま半値幅の悪化につながる一方, 偏心がない方向については1次的にはボケても問題ありません.よってディテクター位置を決める際もその偏心がある方向(メリジオナル面)に結像するように式(2)を使って配置します. もちろんトロイダルレンズのような光学系を使うことも有効です.

フォーカシングミラーは必要か

フォーカシングミラーは絶対に必要というわけではありません. 凹面回折格子分光器というのもありますし, 市販の分光ではあまり用いられませんが以下の図の通り, コリメーターミラーで収束させた光束を回折格子に照射させてそのまま波長ごとに像面に集光させる設計もあります.

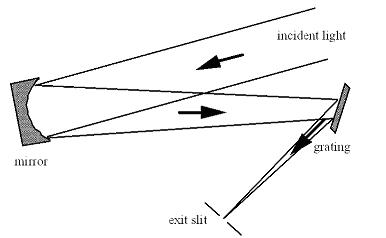
あまり結像性能は良くありませんが, そこに目をつぶれば分光器として使えるといえば使えます.*1

また別の観点としてなぜフォーカシングミラー無しでそしてフラウンホーファー近似無しでフラウンホーファー回折が実現できるか疑問に感じるかもしれません. チェルニターナーの場合はカメラミラーによるフーリエ変換作用によりフレネル回折をフラウンホーファー回折にすることができたわけです. このことをフーリエ光学の観点から次の以前の記事も参考にしながら考えていきます.

eikonal.hatenablog.jp

以下の通り距離z離れた平面のある位置に収束している波面が開口によってさえぎられた時のフレネル回折の式を考えてみます.

以前の記事の表記を基本的に踏襲するとして, 前回記事式(1-1)のところがフレネル回折として $r=\sqrt{Z^2+(X-x)^2+(Y-y)^2} \approx Z(1+(X-x)^2 /2Z^2+(Y-y)^2 /2Z^2)$ とし以下の式にまとめるのがいわゆるフレネル回折の結論です. ここからさらに一定の近似をすることでフラウンホーファー回折が得られたわけです.

$\displaystyle u_{P}(X,Y) = \frac{A}{i λZ} \exp(ikZ) \int\int_{U} f(x,y) \exp\left(ik \frac{(X-x)^2+(Y-y)^2}{2Z}\right) dx dy \tag{3-1} \label{3-1}$

今回はこのままフレネル回折のまま考えるとして, ここにさらに収束波の開口上の位相分布を考えますが, この時距離ベクトルrは

$r_U=\sqrt{Z^2+X^2+Y^2} \approx Z+\frac{X^2}{2Z}+\frac{Y^2}{2Z} \tag{3-2} \label{3-2}$

となるので開口上の波面の位相項は $\exp(-ikr_U)$ で表されます.

これをそのまま代入すると式(3-1)の開口関数tにのるとするとフレネル回折式は以下のとおりとなります.

$\displaystyle u_{P}(X,Y) = \frac{A}{i λZ} \exp(ikZ) \int\int_{U} f(x,y) \exp(-ikr_U) \exp\left(ik \frac{(X-x)^2+(Y-y)^2}{2Z}\right) dx dy \\ =\frac{A}{i λZ} \exp(ikZ) \int\int_{U} f(x,y) \exp\left(-ik(Z+\frac{X^2}{2Z}+\frac{Y^2}{2Z})\right) \exp\left(ik \frac{(X-x)^2+(Y-y)^2}{2Z}\right) dx dy \tag{3-3} \label{3-3}$

この式の計算を進めると最終的に,

$\displaystyle u_{P}(X,Y) =\frac{A}{i λZ} \exp\left(ik \frac{X^2+Y^2}{2Z}\right) \int\int_{U} f(x,y) \exp\left(-ik \frac{xX+yY}{Z}\right) dx dy \tag{3-4} \label{3-4}$

となりますが, つまり開口上の座標(x,y)の2次の項が収束光の位相成分とキャンセルされるため, フラウンホーファー近似の結果と同じく積分の中身のexpは(x,y)の1次式で表され, フラウンホーファー回折となるというわけです.

*1:入射光束は平行が好ましいというのは理論的に示すことはできますがそれはまた別の機会で.